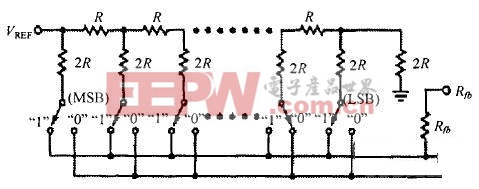
倒置R-2R梯形网络的DAC是由如图2的一个倒置R-2R梯形网络和由数码操控的单刀双置开关组成的。当像图1那样在梯形网络之后级联一个运算放大器,数码操控的单刀双置开关在两个方位切换时不管那一边的电位都是0。因而倒置R-2R梯形网络的VREF端到地的电阻总是R,第i个单刀双置开关上的电流为VREF/(2iR)通过运放后这个单刀双置开关能操控电压为-VREF/2i (Rfb=R时)。
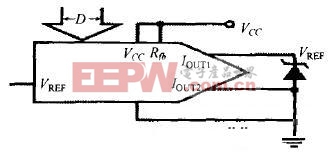
从图1中能够正常的看到,DAC最常见的运用方法是用电流作为转化途径的,这样在DAC之后有必要接一个运放将电流转化为电压才能够正常的运用。而假如如图3所示将DAC0832反过来运用,从两个电流输出端输入电压,即可直接从基准电压输入点直接得到转化电压,而无须再加一级运放。从参阅电压端得到的电压为VREF×D/2n(D为数字输入的值,n为DAC的位数),现证明之。
当有一个或多个数码操控的双置开关放到“1”的方位时,它们与IOUT1连通即和高电平(Vin即Iout1端的电平)连通。依据线性电路的叠
加定理VREF端的电压等于各个与高电平联通的点别离与高电平联通时VREF上的电压之和。这个出题等价于当第p个开关放到“1”的方位时参阅电压脚输出的电平Vp=2-p×Vin即可。当第P个开关(恣意)与高电平联通时电路如图4所示。
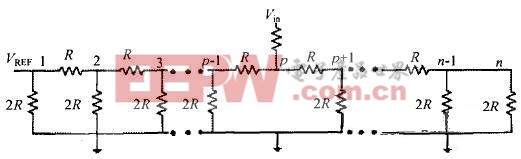
用数学归纳法证明之,假定上述出题建立。当最高位(MSB)与高电平接通时明显最高位的右边仍是一个梯形网络,电阻为2R,故输出电压为2-1×Vin,满意假定。当第P与高电平接通时,如图4设梯形网络中阻值为R的各个电阻之间的点为1,2,,n,n-1这些以左的电阻对地的阻值为R1,R2,,Rn。则能够取得Ri与Ri+1之间的递推联系是:Ri+1等于(Ri+R)并联上2R,即:
被接到高电平的电阻右边的网络阻值始终是2R,故总能够把它简化为一个阻值为2R的电阻则:
第p+1个电阻被接到Vin时,由式(2)得到Vp+1,再将式(2)代入Vp+1。得:

